在机器学习以及深度学习中我们经常会看到正则化这一名词，下面就浅谈一下什么是正则化？以及正则化的意义所在？

一、什么是正则化？

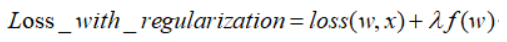
正则化项 (又称惩罚项)，惩罚的是模型的参数，其值恒为非负
λ是正则化系数，是一个超参数，调节惩罚的力度，越大则惩罚力度越大。

二、正则化的目的？

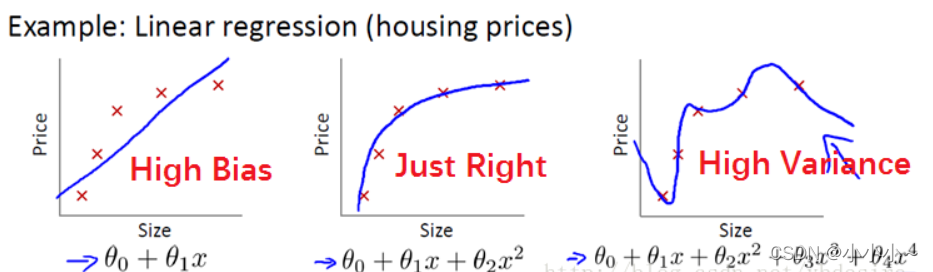
先上图：
上图从左到右依次为：欠拟合、理想状态、过拟合
欠拟合从字面意思来看就是欠缺拟合程度，这一般在复杂度很低的模型中出现。从数学上来看，一元一次函数为一条直线、一元二次函数为一个曲线，以此类推。那么参数越多，其越能拟合更复杂的特征，但是一味的增加模型的复杂度就会造成过拟合现象。一旦过拟合，模型的泛化能力以及鲁棒性将特别差。那么怎么结局过拟合现象呢？
在从数学方面分析来看，为了减小过拟合，要将一部分参数置为0，最直观的方法就是限制参数的个数，因此可以通过正则化来解决，即减小模型参数大小或参数数量，缓解过拟合。
在神经网络中，激活函数（以sigmoid为例）如下图

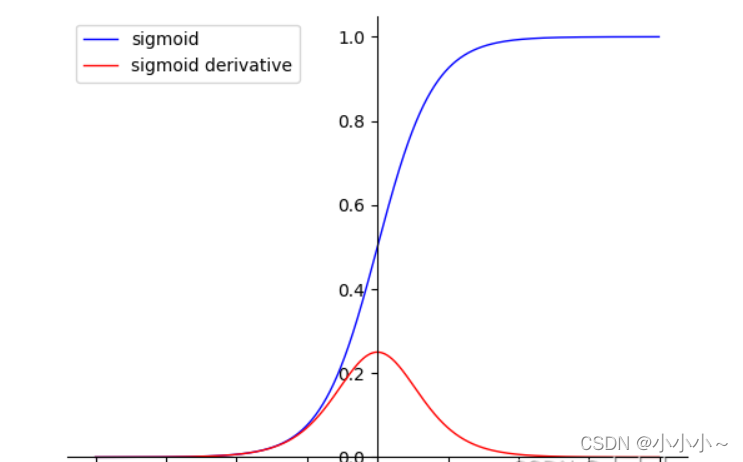
如果我们的正则化系数（lambda）无穷大，则权重w就会趋近于0。权重变小，激活函数输出z变小。z变小，就到了激活函数的线性区域，从而降低了模型的非线性化程度。

三、L1和L2正则化

（一）L1正则化

L1正则化,又称Lasso Regression，是指权值向量w中各个元素的绝对值之和。比如 向量A=[1，-1，3]， 那么A的L1范数为 |1|+|-1|+|3|。
L1正则化可以让一部分特征的系数缩小到0，所以L1适用于特征之间有关联的情况可以产生稀疏权值矩阵（很多权重为0，则一些特征被过滤掉），即产生一个稀疏模型，可以用于特征选择。L1也可以防止过拟合。
那么L1为什么会产生一个稀疏权值矩阵呢？
L1正则化是权值的 绝对值之和，所以L1是带有绝对值符号的函数，因此是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数后添加L1正则化项时，相当于对损失函数做了一个约束。

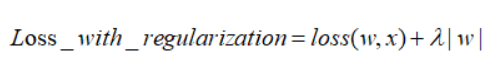
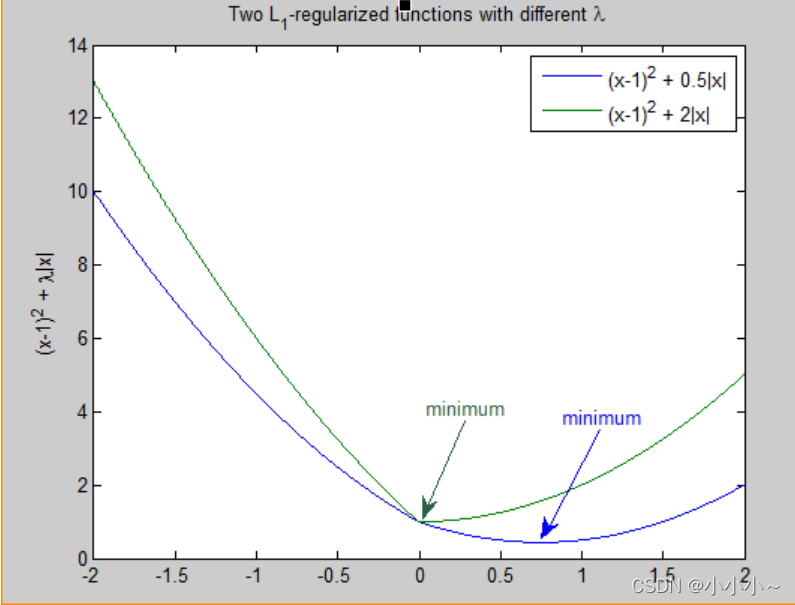
此时我们的任务变成在约束下求出取最小值的解。考虑二维的情况，即只有两个权值和 ，此时对于梯度下降法，求解函数的过程可以画出等值线，同时L1正则化的函数也可以在二维平面上画出来。如下图：

(1)、从优化问题来看

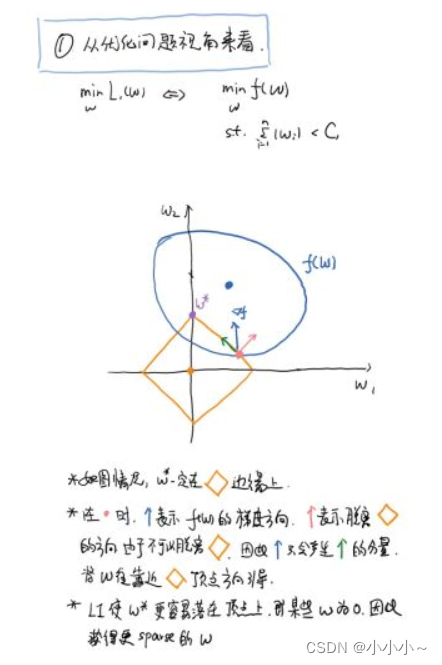
上面的图不是很清楚，补充如下：

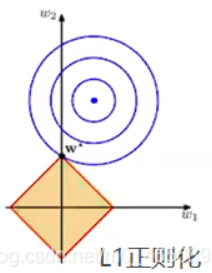
图中蓝色圆圈线是Loss中前半部分待优化项的等高线，就是说在同一条线上其取值相同，且越靠近中心其值越小。
黄色菱形区域是L1正则项限制。带有正则化的loss函数的最优解要在黄色菱形区域和蓝色圆圈线之间折中，也就是说最优解出现在图中优化项等高线与正则化区域相交处。从图中可以看出，当待优化项的等高线逐渐向正则项限制区域扩散时，L1正则化的交点大多在坐标轴上，则很多特征维度上其参数w为0，因此会产生稀疏解；而正则化前面的系数，可以控制图形的大小。越小，约束项的图形越大（上图中的黄色方框）；越大，约束项的图形就越小，可以小到黑色方框只超出原点范围一点点，这是最优点的值中的可以取到很小的值。

(二)、L2正则化

L2正则化是指权值向量中各个元素的平方和然后再求平方根，对参数进行二次约束，参数w变小，但不为零，不会形成稀疏解 。它会使优化求解稳定快速，使权重平滑。所以L2适用于特征之间没有关联的情况。
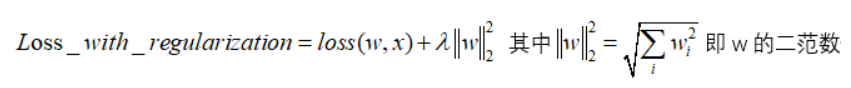考虑二维的情况，即只有两个权值和 ，此时对于梯度下降法，求解函数的过程可以画出等值线，同时L1正则化的函数也可以在二维平面上画出来。如下图：

图中蓝色一圈一圈的线是Loss中前半部分待优化项的等高线，就是说在同一条线上其取值相同，且越靠近中心其值越小。图中黄色圆形区域是L2正则项限制。带有正则化的loss函数的最优解要在loss函数和正则项之间折中，也就是说最优解出现在图中优化项等高线与正则化区域相交处。从图中可以看出，当待优化项的等高线逐渐向正则项限制区域扩散时L2正则化的交点大多在非坐标轴上，二维平面下L2正则化的函数图形是个圆，与方形相比，被磨去了棱角。因此与相交时使得或等于零的机率小了许多，这就是为什么L2正则化不具有稀疏性的原因。

四、两种正则化的不同

（一）、从梯度方面来看

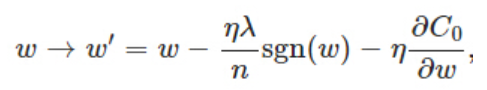
上图分别为(左侧)L1、（右侧）L2正则化的反向传播函数

相对于L1：比原始的更新规则多出了η ∗ λ ∗ s g n ( w ) / n η * λ * sgn(w)/nη∗λ∗sgn(w)/n这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大——因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。
相对于L2：在不使用L2正则化时，求导结果中w前系数为1，现在w前面系数为 1 − η λ / n 1−ηλ/n1−ηλ/n ，因为η、λ、n都是正的，所以 1 − η λ / n 1−ηλ/n1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。当然考虑到后面的导数项，w最终的值可能增大也可能减小。更小的权值w，从某种意义上说，表示模型的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。
综合以上两个式子：当w ww处于[ 1 , + ∞ ] [1, +\infty][1,+∞]时，L2比L1获得更大的减小速率，而当w ww处于( 0 , 1 ) (0,1)(0,1)时，L1比L2获得更快的减小速率，并且当w越小，L1更容易接近到0，而L2更不容易变化。下图反应的更为形象一些。

（二）、概率方面来看